Untuk dapat memahami data dengan mudah, maka baik data kualitatif maupun data kuantitatif harus disajikan dalam bentuk yang ringkas dan jelas. Salah satu cara untuk meringkas data adalah dengan distribusi frekuensi, yaitu pengelompokan data kedalam beberapa kelompok (kelas) dan kemudian dihitung banyaknya data yang masuk kedalam tiap kelas.
A. Distribusi Frekuensi Data Kualitatif
Misalnya kita memiliki data kualitatif 20 orang pemilih untuk tiga partai pilihan, yaitu partai A, B, dan C. Data hasil pilihan 20 orang tersebut adalah sebagai berikut:
A B A A C A A B C B C C B A B C A B B A
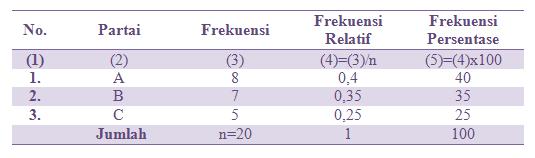
Data di atas dapat kita sajikan kedalam tabel distribusi frekuensi sebagai berikut:
Berdasarkan tabel distribusi frekuensi yang telah disajikan di atas, kita dapat mengetahui bahwa dari 20 pemilih yang ada, paling banyak memilih partai A, yaitu sebanyak 8 orang. Yang memilih partai B sedikit lebih kecil yaitu ada 7 orang. Sedangkan partai C adalah yang pemilihnya paling sedikit, yaitu ada 5 orang.
Distribusi Frekuensi Relatif dan Persentase Data Kualitatif
Distribusi frekuensi menunjukkan jumlah atau banyaknya item dalam setiap kategori atau kelas. Meskipun demikian, kita sering tertarik untuk mengetahui proporsi atau persentase item dalam setiap kelas. Hal ini dapat ditunjukkan dengan frekuensi relatif. Frekuensi relatif dari suatu kelas adalah proporsi item dalam setiap kelas terhadap jumlah keseluruhan item dalam data tersebut. Jika sekelompok data memiliki n observasi, maka frekuensi relatif dari setiap kategori/kelas akan diberikan sebagai berikut:
Sedangkan frekuensi persentase dari suatu kelas adalah frekuensi relatif kelas tersebut dikalikan dengan 100.
Distribusi frekuensi relatif adalah ringkasan dalam bentuk tabel dari sekelompok data yang menunjukkan frekuensi relatif bagi setiap kelas. Distribusi frekuensi persentase adalah ringkasan dalam bentuk tabel dari sekelompok data yang menunjukkan frekuensi persentase bagi setiap kelas. Hubungan antara frekuensi, frekuensi relatif, dan frekuensi persentase dapat ditunjukkan oleh tabel berikut:
B. Distribusi Frekuensi Data Kuantitatif
Definisi tentang distribusi frekuensi adalah sama baik untuk data kualitatif maupun data kuantitatif. Meskipun demikian, kita harus menentukan terlebih dahulu jumlah kelas yang akan dibentuk dalam distribusi frekuensi data kuantitatif. Berbeda dengan data kualitatif yang kelasnya sudah terbentuk berdasarkan kategori-kategorinya. Ada tiga hal yang perlu diperhatikan dalam menentukan kelas bagi distribusi frekuensi data kuantitatif, yaitu jumlah kelas, lebar (interval) kelas, dan batas kelas.
Jumlah Kelas
H.A. Sturges pada tahun 1926 menulis artikel dengan judul: "The Choice of a Class Interval" dalam Journal of the American Statistical Association yang mengemukakan suatu rumus untuk menentukan jumlah kelas sebagai berikut:
k = 1+ 3,322 log n
Dimana: k = jumlah kelas
n = jumlah observasi
Rumus tersebut diberi nama Kriterium Sturges dan merupakan suatu rumus yang menjadi patokan untuk menentukan berapa jumlah kelas yang harus dibentuk dari sekelompok data.
Interval Kelas
Disarankan interval atau lebar kelas adalah sama untuk setiap kelas. Sebenarnya, pemilihan interval kelas dan jumlah kelas tidak independen. Semakin banyak jumlah kelas berarti semakin kecil interval kelas, begitu pula sebaliknya.
Pada umumnya, untuk menentukan interval kelas digunakan rumus:
c = (Xmax - Xmin)/k
Dimana: c = panjang interval kelas
k = jumlah kelas
Xmax = nilai observasi terbesar
Xmin = nilai observasi terkecil
Batas Kelas
Batas kelas bawah menunjukkan kemungkinan nilai data terkecil pada suatu kelas. Sedangkan batas kelas atas mengidentifikasi kemungkinan nilai data terbesar dalam suatu kelas. Jika diketahui kelas-kelas interval adalah 30-39, 40-49, 50-59, dst, maka untuk nilai batas bawahnya (lower limit) adalah 30, 40, 50, dst. Sedangkan nilai batas atasnya (upper limit) adalah 39, 49, 59, dst. Perlu diperhatikan bahwa kelas interval 30-39, 40-49, 50-59, dst, secara teoritis mencakup seluruh nilai interval 29,5-39,5; 39,5-49,5, dst. Nilai-nilai 29,5; 39,5 disebut sebagai tepi bawah kelas (lower class boundary), sedangkan 39,5; 49,5, dst disebut sebagai tepi atas kelas (upper class boundary). Jarak antara tepi atas kelas dan tepi bawah kelas tersebut merupakan panjang interval kelas.
Frekuensi Relatif, Frekuensi Kumulatif, dan Grafik
Seringkali untuk keperluan analisis, selain dibuat tabel frekuensi juga dibuat tabel frekuensi relatif dan kumulatif (untuk analisis tabel), kemudian dibuat grafiknya (untuk analisis grafik). Grafik berupa gambar pada umumnya lebih mudah diambil kesimpulannya secara cepat daripada tabel. Itulah sebabnya data seringkali disajikan dalam bentuk grafik. Pada dasarnya, bentuk tabel frekuensi relatif dan kumulatif dapat dilihat pada tabel berikut:
Grafik dari Tabel Frekuensi, Frekuensi Relatif, dan Kumulatif
Dalam beberapa hal seringkali data dari tabel disajikan dalam bentuk grafik, misalnya dalam bentuk histogram, frekuensi poligon, kurva frekuensi. Untuk membuat histogram, batas-batas kelas diubah terlebih dahulu menjadi tepi atas dan tepi bawah kelas. Untuk contoh di atas, kelas-kelasnya diubah menjadi 22,5-27,5; 27,5-32,5; 32,5-37,5, dst. Kemudian, setiap batangan (bar) dibuat pada kelas-kelas ini dengan tinggi sebesar frekuensi yang bersangkutan.Contoh gambar histogram adalah sebagai berikut:
Apabila titik tengah pada setiap batangan (bar) dihubungkan, maka kita akan memperoleh apa yang disebut poligon atau lengkapnya frequency poligon, seperti gambar berikut:
Apabila tabel frekuensi digambarkan grafiknya, maka akan terlihat suatu kurva. Kurva yang diperoleh itu disebut kurva frekuensi (frequency curve), dan seringkali bentuknya mendekati suatu fungsi tertentu. Kurva frekuensi yang paling terkenal dan sering digunakan dalam statistika adalah kurva normal. Gambar dari kurva normal adalah sebagai berikut:
Kurva Frekuensi Kumulatif (Ogive)
Terdapat dua jenis ogive yaitu ogive "kurang dari" dan ogive "lebih dari". Ogive "kurang dari" dibuat dengan menggunakan tepi atas kelas (upper class boundary) sebagai sumbu absisnya (sumbu-x). Sumbu ordinatnya (sumbu-y) adalah kumulatif dari frekuensi kelas-kelas yang berada di bawah tepi atas kelas. Sedangkan untuk membuat ogive "lebih dari" kita menggunakan tepi bawah kelas (lower class boundary) sebagai sumbu absisnya (sumbu-x). Sumbu ordinatnya (sumbu-y) adalah kumulatif dari frekuensi kelas-kelas yang berada di atas tepi bawah kelas. Contoh gambar dari ogive adalah sebagai berikut:
Kurva Lorenz
Dalam analisis ekonomi, khususnya pada masalah pemerataan pendapatan, dikenal suatu kurva yang disebut Kurva Lorenz (Lorenz Curve). Kurva Lorenz pada dasarnya juga merupakan kurva frekuensi kumulatif. Sumbu absis dari Kurva Lorenz menunjukkan kumulatif jumlah penduduk. Sedangkan sumbu ordinatnya menunjukkan kumulatif pendapatan. Dalam praktiknya, sumbu absis menunjukkan angka persentase kumulatif dari penduduk. Sedangkan sumbu ordinatnya menunjukkan angka persentase kumulatif pendapatan. Idealnya, jika pendapatan terdistribusi secara merata ke seluruh penduduk maka bentuk kurvanya akan mendekati garis lurus (line of equality). Artinya, 1% penduduk menerima 1% pendapatan, 2% penduduk menerima 2% pendapatan, dst. Sebaliknya, jika pendapatan tidak terdistribusi secara merata maka kurva yang terbentuk akan menjauhi garis lurus (line of equality). Gambarnya sebagai berikut:
Pembagian pendapatan yang tidak sama atau kurang merata sering disebut sebagai "income gap", yaitu jurang pemisah antara yang kaya (pendapatan tinggi) dan yang miskin (pendapatan rendah). Apabila income gap makin besar, sering terjadi kekacauan atau paling tidak menimbulkan rasa tidak puas masyarakat, yang kadang-kadang menjurus ke pemberontakan.
Semoga Bermanfaat






sangat membantu dalam belajar terimakasi kang mas
BalasHapus